regression_logistic
pZiel ist es, die Logistische Regression als Spezialfall der MR sowie als einen Anwendungsfall des GLM zu kennenzulernen.
Logistische Regression ist eine Unterform der Gruppe der Generalized Linear Models. Die Link-Funktion des Kriteriums ist die Logit-Transformation.
Ausflug: odds und odds-ratios
odds oder Quote: Verhältnis von Beobachtungen, für die ein binäres Merkmal zutrifft oder nicht (Erkrankte / nicht Erkrankte). Quotient aus der Wahrscheinlichkeit für ein Ereignis durch die Gegenwahrscheilichkeit.
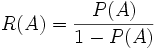
odds-ratio oder Quotenverhältnis: Verhältnis von odds, z. B. wenn ein weiteres binäres Merkmal erfasst ist (Risikofaktor vorhanden / nicht vorhanden). Für beide Risiko-Faktor-Gruppen werden die odds (Erkrankung ja/nein) berechnet und ins Verhältnis zueinander gesetzt.
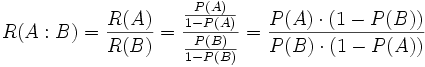
Ausflug Logistische Funktion
logistische Funktion
s-förmige Kurve
Zwei Parameter legen die Kurve fest: Lage des Wendepunktes in x-Werten, Steilheits-Parameter.
Abb:
Konstante ist Verschiebung in X-Richtung, Gewicht ist Steilheit. Die Ähnlichkeit zur MR wird in der vorletzten Formel am deutlichsten, aber da können die beiden Parameter nicht unabhängig voneinander geändert werden, wie in der letzten Formel.
Ausflug Generalisierte Lineare Modelle
Logistische Regression, Allgemeines
Das Kriterium ist hier dichotom/binär. Problem des eingeschränkten Schwankungsbereiches des Kriteriums. Lösungsansatz: Umwandlung durch geeignete Transformation (logit). S-Kurve wie in der Item-Response Theorie.
Dieser Ansatz lässt einen Schluss auf die Wahrscheinlichkeit einer der beiden Ausprägungen zu. Das Festlegen der dichotomen Ausprägung geschieht über einen cut-off-Wert (meist bei 0.5).
Parameterschätzung über die entsprechenden Verfahren ergeben für jede Erklärungsvariable einen Parameter, logit(p).
Die Odds-Ratio (zu interpretieren als Änderung im Kriterium (Response-Variable) pro Einheit in Erklärungsvariable) exp(parameter).
Prüfung Gesamtmodell
Goodness of fit. Analogie zu R2 in MR.
Verschiedene Ansätze. Nur Annäherungen.
log likelihood ratio, -2 log likelihood, Cox / Snell R2, Nagelkerke R2
log likelihood ratio:
Deviance als Äquivalent zu Quadratsummen (bzw. erklärter Varianz) in MR. Ausmaß der Abweichung der Daten in einem logistischen Modell (lack of fit).
Deviancemodel = -2ln [(likelihood fitted model)/(likelihood saturated model)]
Deviancenull = -2ln[(likelihood null model)/(likelihood saturated model)]
saturated model ist ein Modell mit 'theoretisch perfektem Fit'
null model ist Modell nur mit der Konstanten als Prädiktor
Deviancemodel sig. kleiner deviancenull => Fit des Modells ist statistisch besser als Nullmodell.
likelihood-ratio: -2ln[(likelihood null model)/(likelihood fitted model)]
Chi2 zur Prüfung des Gesamtmodells: deviancemodell - deviancenull
analog F-Test in MR.
pseudo-R2
R2 likelihood ratio: R2L = (Dnull - Dmodel)/Dnull
Limitation: R2L ist nicht monoton verbunden mit der odds-ratio
Klassifikationstabelle
Prüfung der Prädiktoren
Wald-Statistik
Probleme:
Verhältnis Variablen zu Vpn
complete separation
Einflussreiche Beobachtungen
Datenfiles
Beispieldatensatz Everitt (2010) zu log. Regr. GHQ-Datensatz (General Health Questionnaire). GHQ-Werte schwanken von 0(gesund) - 10 (krank) Geschlecht (1=Frau, 2=Männer) Anzahl der Fälle, die als psychatrische Fälle klassifiziert wurde. Anzahl der Fälle, die keine psychatrischen Klassifikationen erhielten.
"http://www.psych.uni-goettingen.de/mat/mat/ghq.txt"
sex GHQ ncases nnotcases 0 0 4 80 0 1 4 29 0 2 8 15 0 3 6 3 ... 0 9 2 0 0 10 1 0 1 0 1 36 1 1 2 25 1 2 2 8 ... 1 8 3 1 1 9 2 0 1 10 2 0
Derselbe Datensatz, nur dass die Vpn einzeln aufgeführt sind. Das entspricht der üblichen Struktur der Datensätze.
"http://www.psych.uni-goettingen.de/mat/mv/ghq-vp.txt"
vp sex ghq case cnt 1 1 0 1 1 2 1 0 1 2 3 1 0 1 3 4 1 0 1 4 5 1 0 0 1 ... 167 1 7 1 1 168 1 7 1 2 169 1 8 1 1 170 1 8 1 2 171 1 8 1 3 172 1 9 1 1 173 1 9 1 2 174 1 10 1 1 175 0 0 1 1 176 0 0 0 1 ... 273 0 8 1 3 274 0 8 0 1 275 0 9 1 1 276 0 9 1 2 277 0 10 1 1 278 0 10 1 2
Beispieldatensatz Everitt (2010) zu log. Regr.
do-it-yourself-Datensatz
work (skilled/unskilled/office)
tenure (rent/own)
type (appartment/house)
age (<30/31-45/46+)
yes (Anzahl)
no (Anzahl)
"http://www.psych.uni-goettingen.de/mat/danwork.txt"
work tenure type age yes no 1 skilled rent apartment <30 18 15 2 skilled rent apartment 31-45 15 13 3 skilled rent apartment 46+ 6 9 4 skilled rent house <30 34 28 5 skilled rent house 31-45 10 4 6 skilled rent house 46+ 2 6 7 skilled own apartment <30 5 1 8 skilled own apartment 31-45 3 1 9 skilled own apartment 46+ 1 1 10 skilled own house <30 56 12 ......
Datensatz als Einzel-Vps ...
Logistische Regression in R
Ein Tutorial dazu.
Logistische Regression in Statistica
Logistische Regression
- In Statistica zu finden unter
"Statistik | höhere (nicht)lineare Modelle | nichtlineare Regression | logistische Regression"
wichtig ist, im Dialogfenster nach der Variablenauswahl/Modellspezifikation das Häkchen bei "asymt. Standardfehler" zu setzen, da nur so z. B. die Paramter-Signifikanztests erfolgen. - Alternativ direkt bei GLZ
"Statistik | höhere (nicht)lineare Modelle | verallgemeinerte lineare/nichtlineare Modelle" - Übliche Struktur des Datensatzes mit einer Zeile pro Vp: "Daten enthalten | Codes und keine Häufigkeiten"
Häufigkeitsdaten (Aggregieren über Vpn gleicher Bedingungskombination): "Daten enthalten | Codes und Häufigkeiten" Achtung, das geht nur für Prädiktoren (UV), nicht für Kriterium (AV). - Ergebnis-Überblick im ersten Ergebnisfenster Oberteil (automatisches Umcodieren bei Anzahl)
- 'Zusf: Paramterschätzungen"
oben nochmals Gesamttest
in der Tabelle die Modell-Koeffizienten - 'Beob./Prognose/Residuen'
erzeugt eine Tabelle mit den Prognostizierten Werten und den Residuen, die Originalvariablen können optional dazu gespeichert werden.
hier ist auch erkennbar, wie der cut-off gelegt wird. Erzeugen einer Variable (über 0.5 -> 1, unter 0.5 -> 0) und Kreuztabelle dazu macht die Prognose nachvollziehbar. - Log-Reg ist näher an Klassifikation bietet aber keine Einzel-UV-Signifikanztests
Datensätze
Beispiele
Aufgaben