mr_va
Varianzanalyse als multiple Regression: ALM (Allgemeines lineares Modell)
Ziel ist es, ein Verständnis für die Äquivalenz des varianzanalytischen Ansatzes und der Multiplen Regression zu entwickeln.
Mit ANOVA werden üblicherweise ein- bzw. mehrfaktorielle Designs mit zwei oder mehr Faktorstufen pro Faktor getestet. Dabei wird das Prinzip der Zerlegung in Varianzanteile angewandt. Eine Vpn ist charakterisiert durch die Zugehörigkeit zu einer Faktorstufe oder durch eine Kombination von Faktorstufen. Ermittelt werden die Varianzanteile, die durch die Zugehörigkeit zu Faktorstufen 'erklärt' bzw. 'gebunden' werden Sie werden verglichen mit der durch die Faktoren unerklärten Restvarianz (Residualvarianz).
MR dient der Klärung des Zusammenhanges zwischen intervallskalierten Variablen. Es gibt normalerweise eine Richtung der Erklärung. Eine Kriteriumsvariable wird durch eine oder mehrere Prädiktorvariablen erklärt ('vorhergesagt').
Man kann ANOVA verstehen als die Vorhersage des Kriteriums (AV) aufgrund der Gruppenzugehörigkeit (UV, bzw. Prädiktor). Dabei entsteht das Problem, dass MR Intervallskalenniveau für Prädiktoren voraussetzt. Gruppenzugehörigkeit aber ist eine kategoriale Variable, also ein nominalskaliertes Merkmal.
Prädiktoren sind Indikatorvariablen: Nominalskalierte Variable. Gruppenzugehörigkeit als Dummy-Variable. Beobachtung wird 'Messwert' zugeordnet aufgrund der Gruppenzugehörigkeit. Verschiedene Arten der Dummy-Variablen:
- Dummykodierung
Konstante ist Mittelwert der 0, …, 0 kodierten Variable (Referenzgruppe)
bi Abweichung der Gruppenmittelwerte von der Referenzgruppe
Anwendung: Abweichung mehrer Mittelwerte von einer Kontrollgruppe - Effektkordierung
Konstante ist Gesamtmittelwert
bi Abweichung der Gruppenmittelwerte vom Gesamtmittelwert
Anwendung: Schätzung von Treatmenteffekten, entspricht Varianzanalyse - Kontrastkodierung
Konstante ist Gesamtmittelwert
bi kodieren Kontraste über Kontrastkoeffizienten für Gruppenmittelwerte
Entspricht der Auswertung einer Varianzanalyse mittels Kontrasten
VA Varianzaufklärung: Verhältnis der durch Vorhersagewerte erklärte Varianz zu Gesamtvarianz d. Krit. Übrig bleibt Residuenvarianz (ungeklärte Varianz).

t-Test im ALM
x: 1 1 1 1 -1 -1 -1 -1
y: 8 6 7 9 2 3 2 4
H0: t-Test: Die Mittelwerte der beiden Gruppen unterscheiden sich nicht
H0: ALM: Zwischen den Variablen x und y besteht kein Zusammenhang
Anova mit p Stufen im ALM (Fliegenbeispiel, Effektkodierung)
Einfaktorielle VA mit p=3 Faktorstufen
http://www.psych.uni-goettingen.de/mat/mv/everitt-fly-effect-komma.txt
gn gr y x1 x2
RS 1 12.8 1 0
RS 1 21.6 1 0
...
RS 1 23.6 1 0
SS 2 38.4 0 1
SS 2 32.9 0 1
...
SS 2 10.8 0 1
NS 3 35.4 -1 -1
NS 3 27.4 -1 -1
...
NS 3 47.4 -1 -1
Anova-F-Test

Fliegenbeispiel:
F = MQ Treat / MQ resid.
= 681.1057 / 78.59753
= 8.665739
Anova, erklärte Varianz und Multiples R
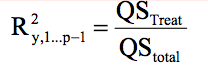
Fliegenbeispiel: R^2 = 681.1057 / (681.1057 + 78.597) = 0.194013
Beispielrechnung Fliegenbeispiel in Statistica
Demonstration der Unterschiede von Referenzkodierung und Effektkodierung an dynamischer Grafik in R-Beispiel
2-faktoriell balanced
Everitt-Beispiel 2x2 Design (A, B), 4 Beobachtungen pro Gruppe
http://www.psych.uni-goettingen.de/mat/mv/everitt-2x2-bal.txt
Effektkodierung für die je beiden Faktorstufen
2-faktoriell unbalanced
Everitt-Beispiel 2x2 Design (A, B), 4 Beobachtungen pro Gruppe
http://www.psych.uni-goettingen.de/mat/mv/everitt-2x2-unbal.txt
Effektkodierung für die je beiden Faktorstufen
Unterschiede, die die verschiedenen Typen von Quadratsummen produzieren
2-faktoriell balanced, 2 x 3 Faktorstufen
generierte Daten, 2 x 3 Design (A, B), 30 Beobachtungen pro Gruppe
http://www.psych.uni-goettingen.de/mat/mv/virtual-2x3-bal.txt
bzw für Statistica
http://www.psych.uni-goettingen.de/mat/mv/virtual-2x3-bal-komma.txt
Lösungsansatz: Dummy-Codierung der Gruppenzugehörigkeit. Dichotome Variablen können behandelt werden wie intervallskalierte. Aufsplittung von mehr als zwei Faktorstufen in (Anzahl-der-Faktorstufen - 1) binäre Dummy-Variablen. Hier demonstriert am Beispiel der Effektcodierung.
Effektcodierung ermöglicht den direkten Vergleich des MR-Ansatzes mit dem ANOVA-Ansatz.
Effektkodierung - Kodierungsprinzip
eine Gruppe/Kategorie auf allen Faktorstufen gleich -1 (z. B. Vergleichsgruppe, KG)
alle anderen Gruppen je auf einer Faktorstufe 1, auf allen anderen Null .
Man braucht also Faktorstufenzahl - 1 Dummy-Variablen zur Kodierung.
2 Faktorstufen/Gruppen 3 Faktorstufen/Gruppen
Dummy Variable x1 x1 x2
Faktorstufe 1 1 1 0
Faktorstufe 2 -1 0 1
Faktorstufe 0(3) -1 -1 (z.B. KG)
Unter http://www.ats.ucla.edu/stat/mult_pkg/faq/general/effect.htm finden sich nähere Erklärungen zu Effektcodierung und dem Unterschied zu reiner Dummy-Codierung.
Siehe auch die Dummy-Codierungs-Seite.
Der MR-Ansatz ist ein eleganter Ansatz, weil damit das Problem der Überparametrisierung vermieden werden kann. Spezifischere Hypothesen können überprüft werden. Bei unbalanced-Designs kann die Reihenfolge kontrolliert werden.
ANOVA hat das prinzipielle Problem, dass Überparametrisierung nur gelöst werden kann über die Zusatzannahme, dass die Summe der Effekte (Abweichungen vom Grand-Mean) 0 ergeben muss. Mit MR können sehr flexibel Parameter aufgenommen oder weggelassen werden (flexible Modellspezifikation). Ausserdem kann man bei dem MR-Ansatz die Reihenfolge der Effekte in das Modell festlegen und dadurch Einfluss darauf nehmen, welche Effekte sich wann an der noch zu Verfügung stehenden Varianz 'bedienen' dürfen. Standardvorgabe in vielen Statistikpaketen ist, dass zuerst die Interaktionsterme eingehen, was oft sinnvoll ist aber nicht unbedingt immer.
Einfaktorielles zweistufiges Design (T-Test)
Beispiel/Aufgabe:
Am Beispiel Autowaschzeiten erklärt durch Extroversion und Geschlecht (T-Test als einfaktorielle VA mit zwei Ausprägungen via MR)
Beispiel/Aufgabe
Fruchfliegen-Datensatz. Äquivalenz der beiden Ansätze (ANOVA 1-faktoriell, dreistufig)
Beispiel/Aufgabe
Daten von Everitt 2 * 2 balanced 4 Beobachtungen / Gruppe
ANOVA 2 * 2 balanced Design
Beispiel/Aufgabe
selbstgenerierter Datensatz ANOVA 2 * 3 balanced, 20 Beobachtungen / Gruppe
Codierung
Codierungsprinzipien und Beispiele hier
Datenfiles
angelehnt an die Everitt-Beispiele
Fruchtfliegen (ein Faktor, 3 Ausprägungen)
Fruchtfliegen mit dummy Codes (effektkodiert)
2x2 Design Everitt: zweifaktorielles Design, zwei Ausprägungen auf beiden Faktoren, balanced und unbalanced
2x3 Design generierte Daten, zweifaktorielles Design, balanced und unbalanced
Multiple Regression und VA im Vergleich in R
Ein Tutorial dazu.
Aufgaben
Bitte vollziehen Sie die Beispiele von Everitt (2010) hierzu nach und versuchen Sie, die jeweiligen Koeffizienten, Quadratsummen etc. in den beiden Vorgehensweisen (MR und VA) in den Outputs des verwendeten Programms zu identifizieren.
Fruchtfliegen
2*2 Design balanced
2*2 Design unbalanced
Können Sie die Unterschiede der verschiedenen Quadratsummen-Typen identifizieren?
Versuchen Sie eine geeignete Auswertung des Datensatzes virtuell-2x3.txt
---------------
Gleiche bewirkt additive Effekte. Ungleiche Zellenbesetzung führt zu Abhängigkeiten und dies wiederum zur Wichtigkeit der Reihenfolge der Aufnahme der Effekte (welchem Effekt wird die Covarianz zugewiesen).